Leetcode 684. Redundant Connection

题目大意：给我们一个无向图，让我们删掉组成环的最后一条边

In this problem, a tree is an undirected graph that is connected and has no cycles.

The given input is a graph that started as a tree with N nodes (with distinct values 1, 2, ..., N), with one additional edge added. The added edge has two different vertices chosen from 1 to N, and was not an edge that already existed.

The resulting graph is given as a 2D-array of edges. Each element of edges is a pair [u, v] with u < v, that represents an undirected edge connecting nodes u and v.

Return an edge that can be removed so that the resulting graph is a tree of N nodes. If there are multiple answers, return the answer that occurs last in the given 2D-array. The answer edge [u, v] should be in the same format, with u < v.

Example 1:

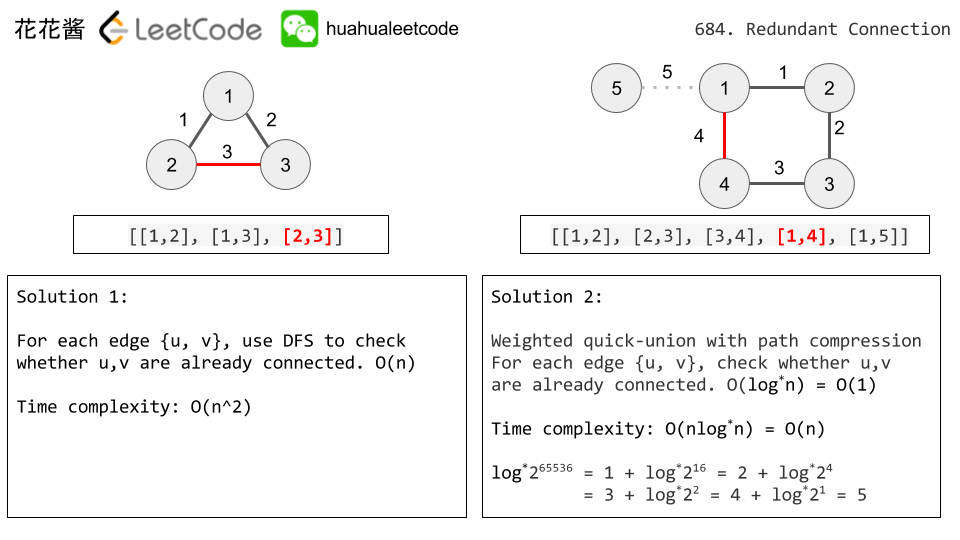
Input: [[1,2], [1,3], [2,3]]

Output: [2,3]

Explanation: The given undirected graph will be like this:

  1
 / \
2 - 3

Example 2:

Input: [[1,2], [2,3], [3,4], [1,4], [1,5]]

Output: [1,4]

Explanation: The given undirected graph will be like this:

5 - 1 - 2
    |   |
    4 - 3

Note:

• The size of the input 2D-array will be between 3 and 1000.
• Every integer represented in the 2D-array will be between 1 and N, where N is the size of the input array.

Difficulty:Medium

Category:

Solution

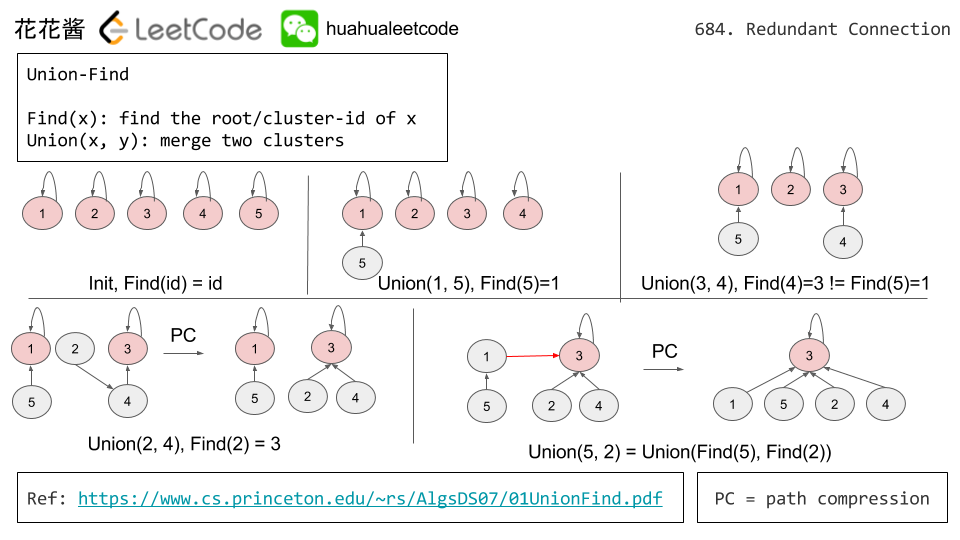
Solution 1: Union Find

Cite: 花花酱 LeetCode 684. Redundant Connection

class UnionFindSet {
 public:
  UnionFindSet(int n) {
    parents_ = vector<int>(n + 1, 0);
    ranks_ = vector<int>(n + 1, 0);

    for (int i = 0; i < parents_.size(); ++i) parents_[i] = i;
  }

  bool Union(int u, int v) {
    int pu = Find(u);
    int pv = Find(v);
    if (pu == pv) return false;

    if (ranks_[pu] > ranks_[pv]) {
      parents_[pv] = pu;
    } else if (ranks_[pv] > ranks_[pu]) {
      parents_[pu] = pv;
    } else {
      parents_[pu] = pv;
      ++ranks_[pv];
    }

    return true;
  }

  int Find(int id) {
    if (id != parents_[id]) parents_[id] = Find(parents_[id]);
    return parents_[id];
  }

 private:
  vector<int> parents_;
  vector<int> ranks_;
};

class Solution {
 public:
  vector<int> findRedundantConnection(vector<vector<int>>& edges) {
    UnionFindSet s(edges.size());

    for (const auto& edge : edges) {
      if (!s.Union(edge[0], edge[1])) return edge;
    }
    return {};
  }
};