Question

You are climbing a stair case. It takes n steps to reach to the top.

Each time you can either climb 1 or 2 steps. In how many distinct ways can you climb to the top?

Note: Given n will be a positive integer.

Example 1:

Input: 2 Output: 2 Explanation: There are two ways to climb to the top.

1. 1 step + 1 step
2. 2 steps

Example 2:

Input: 3 Output: 3 Explanation: There are three ways to climb to the top.

1. 1 step + 1 step + 1 step
2. 1 step + 2 steps
3. 2 steps + 1 step

Difficulty:Easy

Category:DP

Analyze

假设f(n)表示爬到n阶阶梯，的不同方法数量，为了爬到第n阶阶梯，有两种情况：

• 从第n-1阶前进1步
• 从第n-1阶前进2步

所以这就可以得到：f(n) = f(n-1) + f(n-2) 这就是一个斐波那契数列，所以这一个题目相当于是求解第n个参数的数值。

方案二： 斐波那契数列的第n项计算公式为：

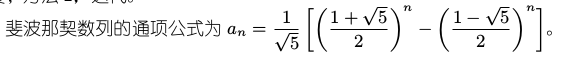
Solution

Solution 1: Top-Down Dynamic Programming(Or Memoization)

class Solution {
 public:
  int climbStairs(int n) {
    vector<int> rec(n + 1, 0);
    return climbStairs(n, rec);
  }

 private:
  int climbStairs(int n, vector<int>& rec) {
    if (n <= 0) return n == 0;

    if (rec[n] == 0) rec[n] = climbStairs(n - 1, rec) + climbStairs(n - 2, rec);
    return rec[n];
  }
};

Buttom-Up Dynamic Programming

class Solution {
 public:
  int climbStairs(int n) {
    if (n <= 1) return n >= 0;

    vector<int> rec(n, 1);　// rec[0] = 1, rec[1] = 1
    for (int i = 2; i < n; ++i) rec[i] = rec[i - 1] + rec[i - 2];
    return rec[n - 1] + rec[n - 2];
  }
};

We don't need the meno[n], we use a, b:

class Solution {
 public:
  int climbStairs(int n) {
    int prev = 0;
    int cur = 1;
    for (int i = 1; i <= n; ++i) {
      int temp = cur;
      cur += prev;
      prev = temp;
    }
    return cur;
  }
};

Solution 2:使用公式直接计算

class Solution {
 public:
  int climbStairs(int n) {
    const double s = sqrt(5);
    return floor((pow((1 + s) / 2, n + 1) + pow((1 - s) / 2, n + 1)) / s + 0.5);
  }
};

Other Question

如果將这个题目稍微修改一下:

Triple Step: A child is running up a staircase with n steps and can hop either 1 step, 2 steps, or 3 steps at a time. Implement a method to count how many possible ways the child can run up the stairs.

Let's think about: What is the lastest step that is done: The very last step: 3-step hop, a 2-step hop, or 1-step hop.

How many ways then are there to get up to the n-th step? We can get up to the n-th step by any of the following.

• Going to the (n -1)-st step and hopping 1 step;
• Goint to the (n-2)nd step and hopping 2 steps;
• Going to the (n-3)rd step and hopping 3 steps;

Then, We just need to add the number of these paths together.

Solution

Solution 1: Brute Force Solution

First, the fairly straightforward algorithm to implement recursively, followed logic:

countWays(n-1) + countWays(n-2) + countWays(n-3)

There is a quesiton: what is countWays(0)? Is it 1 or ) It's a lot earier to define it as 1.

Implementation code.

int countWays(int n) {
  if(n < 0) return 0;
  else if (n == 0) return 1;
  else {
    return countWays(n - 1) + countWays(n - 2) + countWays(n - 3);
  }
}

Like the Fibonacci problem, the runtime of this algorithm is exponential($O(3^n)$).

Solution 2: Add Memoization in this Solution 1

The previous solution for countWays is called many times for the same values, which is unnecessary. We need to fix it.

class Solution {
 public:
  int climbStairs(int n) {
    vector<int> rec(n + 1, -1);
    return countWays(n, rec);
  }

 private:
  int countWays(int n, vector<int>& rec) {
    if (n < 0) return 0;
    else if (n == 0) return 1;
    else if (rec[n] > -1) {
      return rec[n];
    } else {
      rec[n] = climbStairs(n - 1, rec) + climbStairs(n - 2, rec) + climbStairs(n - 3, rec);
      return rec[n];
    }
};